用TensorFlow寻找两条曲线的关系

发表于 更新于 分类于 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

前言

在上一篇文章中，我们创建了数据集，然后探究了怎么对齐数据，接下来就简简单单拟合一下。

构建模型

首先，我们查到，最适合拟合的就是LSTM，所以我们直接一个构建：

1
2
3
4
5
6
7
import tensorflow as tf
model = tf.keras.models.Sequential([
  tf.keras.layers.LSTM(units = 144, dropout = 0.2, activation = 'softmax', input_shape = (750, 1)),
  tf.keras.layers.Dense(units = 1, activation = 'elu')
])
model.compile(optimizer = 'adam', loss = tf.keras.losses.mean_squared_error)
model.build(input_shape = (None, 750, ROW_SIZE))

这里面其实有这么一些要点可以关注：

首先，模型的第一层就是LSTM，既不需要Flatten层，也不需要Dense层，直接处理就好；其中，input_shape主要是为了配合当前的数据集，dropout主要是为了防止过拟合。

其次，模型的第二层就直接输出，也就是Dense层。因为是直接输出，所以对应的是有且只有$z$，也就是数量是$1$。

P.S.：激活函数在这里并没有什么原因，我是靠点兵点将点出来的。(,,・ω・,,)

当然啦，激活函数的选择确实有考究，但是因为这只是一个特别理想的案例，所以就不那么纠结了。

最后呢，优化器选择的是mean_squared_error，也就是均方误差。用这个名字你可能不太认识，但我换一个你应该就认识了。他就是：MSE。

既然模型已经搭建好了，我们试着查看一下模型信息：

1
model.summary()

于是就输出了：

1
2
3
4
5
6
7
8
9
10
11
12
13
Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 lstm_1 (LSTM)               (None, 144)               84096     
                                                                 
 dense_1 (Dense)             (None, 1)                 145       
                                                                 
=================================================================
Total params: 84,241
Trainable params: 84,241
Non-trainable params: 0
_________________________________________________________________

看着不错，参数量很大。

训练数据

也就是说，咱就是每一段数据都有成对的$y$和$z$用来训练？

那还不简单嘛。直接用pandas把一共$50$组的$y$和$z$全部放在pandas中，每一组用pandas的索引区分；最后，pandas的每一个单元格存放的是列表。

这样的话，如果需要访问第$i$组的$y$所构成的列表，也就只需要这样访问：

1
df.loc[i, 'y']

假设我完全不懂什么深度学习，我也大概可以弄出来一个训练过程：

1
2
3
4
for index in range(40):
  X_train = df.loc[index, 'x'].to_numpy()
  y_train = df.loc[index, 'y'].to_numpy()
  model.fit(X_train, y_train, epochs = 3)

看着很合理。

每组数据训练$3$次，一共取$50\times80%=40$组数据进行训练，最后使用$50\times20%=10$进行测试。

训练加速

但是啊，训练的时候还是因为for循环引入了太多了CPU操作。这就像是在游乐园排队一样，每个人上去玩$3$把，玩完立刻下来，中间虽然有CPU在指挥，但$40$组数据就这么排着队，一个个等着上去玩。

这不太好。

该怎么办呢？

我们曾经刚开始接触C语言的时候，往往就是用循环实现一个矩阵乘法之类的。后来接触了Python才知道，原来大规模矩阵的乘法可以这么快。

诶！你说，矩阵运算会不会快很多？

因为，这次就像考试一样，安排所有人全部进去，然后统一开始，统一回收结果，最后全部排名。看着高效多了！

于是我们再来一次：

1
2
3
4
TRAIN_SIZE = int(y.shape[0] * 0.8)
X_train = y[:TRAIN_SIZE, :, np.newaxis]
y_train = z[:TRAIN_SIZE, :, np.newaxis]
model.fit(X_train, y_train, epochs = 100)

这就相当于，本来有$50$组数据，取$40$组，每组全量数据拿过来作为训练集，并且为了对应输出的维度，增加一个np.newaxis。于是本来二维的数据成了三维。

这样一练就快多啦！

再次加速

其实这没什么别的技巧，就是单纯的把这玩意儿放到显卡去。

训练结果

到这一步，我们也就能看到结果了：

训练结果

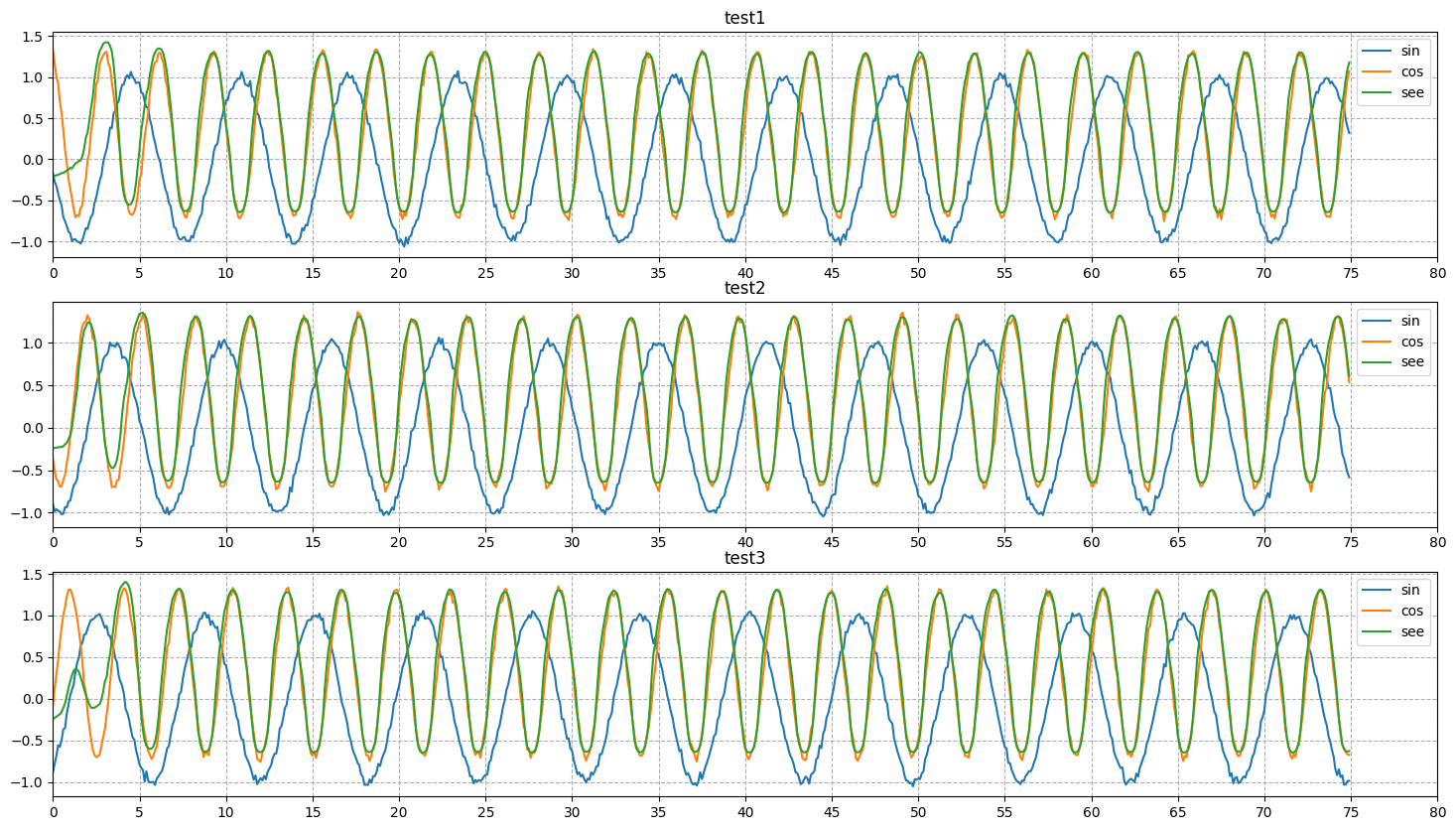
可以看到，大致上拟合还是不错的，就只是当$x$在$[0,2]$左右的时候，拟合效果并没有特别好，后面还是基本都重合了的。

彩蛋

在上一篇文章中中，我只存放了一个截图，表示用时间片对应着训练的时候效果并没有很好。

其实吧，大概是这样的：

我用的是训练很慢的那一套，用一个时间片分割出来一段段短序列，再用短序列去预测。

1
2
3
4
5
6
7
8
9
10
11
12
TRAIN_SIZE = int(len(raw_data) * 0.85)
for index in range(TRAIN_SIZE):
  train_temp = raw_data.loc[index, :].copy()
  LENGTH = len(train_temp['y'])
  X_train, y_train = [], []
  for i in range(LENGTH - TIME_STEP):
    X_train.append([item for item in train_temp['z'][i : i + TIME_STEP]])
    y_train.append(train_temp['data_out'][i + TIME_STEP])
  X_train = np.array(X_train)
  y_train = np.array(y_train)
  X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], 1)
  model.fit(X_train, y_train, epochs = 3)

从结论上来说，大致上像是那么回事：

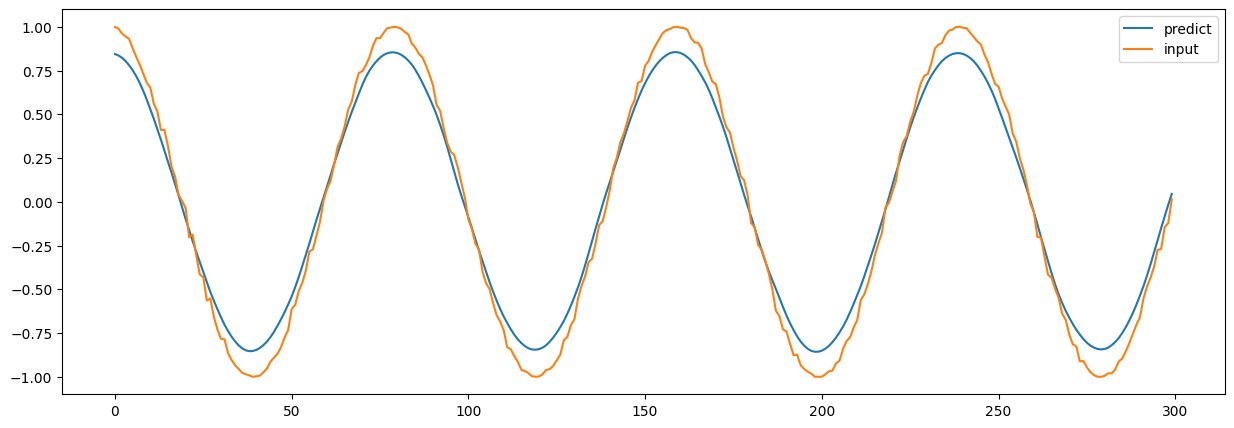
误打误撞的拟合

但实际上，正确率只有惨淡的$1.1941240169107914%$，可以说是哪怕让任意一个人在$[0, 1]$之间蒙$750$次，准确率都比这个高。

当然，这是因为数据本身是很有特点的，每个波峰都是一致的$0$和$1$。当波峰存在差异的时候，效果就非常明显了：

波峰差异

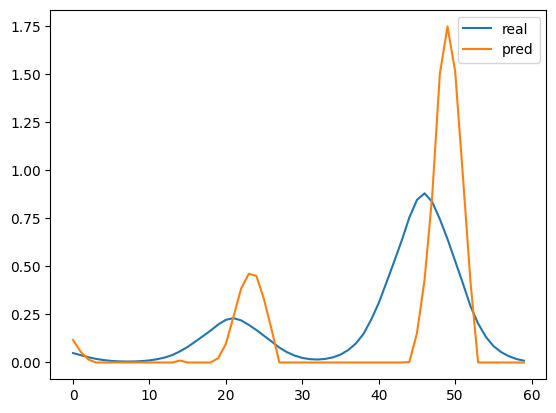
简直就是灾难。