自相关在曲线拟合过程中表现出来的重要作用

前言

在上一篇文章中，我们采用滑动窗口拟合曲线，但是效果很差。其实，这里面就是自相关在起作用。本文从理论角度给出解答。

LSTM在曲线拟合的作用

为了理解这一点，我们先从LSTM开始。首先我们要了解的是，为什么偏偏LSTM在曲线拟合过程中作用明显，但是线性回归的作用并不明显。

线性回归

那我们回顾一下吧，线性回归到底是什么样子的。

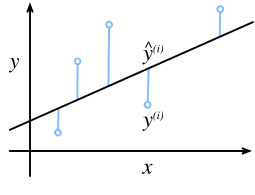
图片转自《动手学习深度学习》（在线版），其源码在GitHub上，点击这里跳转。

顾名思义，线性回归就是用直线$Ax+By+C=0$来描述一系列离散点的规律。而他的估计方式其实就是大学高等数学中必考的最小二乘法。

这个公式其实我们也算是耳熟能详了。对于样本中的随机$n$个样本，平方误差值$\epsilon$为

$$\epsilon=\sum^n_{i=1}\frac{\left(\hat{y}^{(i)}-y^{(i)}\right)^2}{2}\tag{1}$$

LSTM

那么LSTM有什么不同吗？下面这张图就是他的架构：

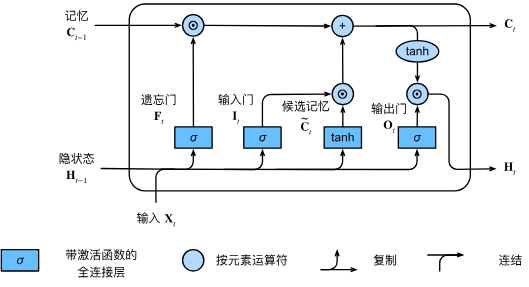
图片转自《动手学习深度学习》（在线版），其源码在GitHub上，点击这里跳转。

对于第$t$时刻输入的信息$\mathbf{X}_t$，每个逻辑门的计算公式实际上就是$\mathbf{X}t$和$\mathbf{X}{t-1}$之间的距离，也就是：

$$
\begin{matrix}
\mathbf{I}t&=&\sigma
\left(
\mathbf{X}t\mathbf{W}{xi}+\mathbf{H}{t-1}\mathbf{W}_{ih}+\mathbf{b}i
\right)\
\mathbf{F}t&=&\sigma
\left(
\mathbf{X}t\mathbf{W}{xf}+\mathbf{H}{t-1}\mathbf{W}{hf}+\mathbf{b}f
\right)\
\mathbf{O}t&=&\sigma
\left(
\mathbf{X}t\mathbf{W}{xo}+\mathbf{H}{t-1}\mathbf{W}{ho}+\mathbf{b}_o
\right)\
\end{matrix}\tag{2}
$$

其中，$\mathbf{W}{xi}$、$\mathbf{W}{xf}$、$\mathbf{W}_{xo}$代表LSTM中每一个门的权重参数，维度其实也相对比较直观，考虑$\mathbf{X}_t$是一个带有$d$个元素的顺序数组，隐藏层单元数量为$h$，那么权重参数的矩阵尺寸为$(d,h)$。同理，二维甚至高维数组的矩阵尺寸依然是这个，因为原本的顺序数组与权重参数是$(1, d)\times(d, h)$，而高维不过是成了$(k, d)\times(d, h)$。

同样的，$\mathbf{b}_i$、$\mathbf{b}_f$、$\mathbf{b}_o$这三个是每个门的偏置，类似于$y=kx+b$中的$b$。正因为他是门的偏执，门的权重矩阵尺寸为$(d,h)$，$\mathbf{b}$的尺寸也不过是给每个输入进去的$\mathbf{x}_t$给出一个偏置系数，所以与$\mathbf{x}_t$的尺寸相同。当$\mathbf{x}_t$为$(1,d)$时，$\mathbf{b}$的尺寸也是$(1,d)$。

也就是说，当输入$\mathbf{x}_t$的时候，LSTM会首先遗忘，然后把记忆拉一个候选$\widetilde{\mathbf{C}t}$，再和以前的记忆$\mathbf{C}{t-1}$合并，最终输出$\mathbf{C}_t$。即：

$$\mathbf{C}_t=
\mathbf{F}t\odot\mathbf{C}{t-1}+\mathbf{I}_t\odot\widetilde{\mathbf{C}_t}\tag{3}
$$

展开为：

$$\mathbf{C}t=
\left(
\begin{matrix}
\sigma\left(
\mathbf{X}t\mathbf{W}{xf}+\mathbf{H}{t-1}\mathbf{W}{hf}+\mathbf{b}f
\right)
\odot
\mathbf{C}{t-1}
\
+
\
\sigma\left(
\mathbf{X}t\mathbf{W}{xi}+\mathbf{H}{t-1}\mathbf{W}{ih}+\mathbf{b}i
\right)
\odot
\tanh\left(
\mathbf{X}t\mathbf{W}{xc}+\mathbf{H}{t-1}\mathbf{W}{hc}+\mathbf{b}_c
\right)
\end{matrix}\right)\tag{4}
$$

P.S.：一行肯定是不够了，就这样折下来，虽然不规范，但希望各位看得懂(っ´ω`c)

所以，正如式$4$所示，新的输出本质上除了每个门的权重以外，还有上一个时间片的记忆，也有这个时间片的输出。

LSTM的作用总结

说到这一步，其实基本上已经清楚了。

对于线性回归，有一个最大的前提，就是用于计算的样本是通过随机采样获得的。而随机采样一定会破坏原有序列的时间顺序，计算过程也就没办法顾及到样本的先后顺序。

就拿周期函数来说，我们对于周期性的定义，根据这篇文档，是指相同的事情以以固定的时间间隔重复，也就是说，样本一定会带有时间特征。既然线性回归没有办法照顾到样本的时间特征，时间信息在最小二乘中被丢弃了，所以线性回归在周期函数中没能表现出较好的拟合能力。

而LSTM不一样，LSTM的计算公式（式$3$）就注定了他在输出的时候是考虑到了之前的信息，也就是一定会照顾到样本的时间特征。

自相关性

上面讨论的这种时间特征，就是样本的自相关性。

根据IBM的定义，自相关性指的就是时间序列中同一变量在不同时间点的相关性。

也就是说，对于函数$y=f(x)$而言，他的信息表面上只有$x$，每一个$x$也都有唯一一个确定的$y$。但是，他的计算过程并不是单一的，而是迭代的，就像是$y=f_n(f_{n-1}(f_{n-2}(…(f_1(x)))))$。在第$t$时刻需要求解$f_t(x)$的时候，永远都需要优先求解$f_{t-1}(x)$，直到找到$f_1(x)$。

更进一步的说，在上一篇文章中，滑动窗口效果并没有增强数据本身的自相关性，反而还因为没有照顾到整条数组的连续性时间特征，导致丢失了整条数据在更广泛意义上的周期性。

就好比说，明明周期$T=2\pi$，最起码也得取$2k\pi$（$k$是正整数），甚至取整条数据；但到最后时间窗口取的是$10$，就相当于只看到了$y=sin(x)$中的一个上半周期、一个下半周期，还有一半的上半周期。在没有看到好多个相同的周期时，就连人脑智能都难以确定是不是$y=sin(x)$。即，当没有完全看到相同的一个完整周期，分析的时候就丢失了这种自相关性。