自相关性检测的小技巧

发表于 分类于 阅读次数： 本文字数： 815 阅读时长 ≈ 3 分钟

前言

在上一篇文章中，我们探讨了自相关性的影响。这次我们在尝试一下，在拟合曲线之前，自相关性有没有什么检测方法。

Durbin-Watson

在IBM的介绍中，有一个Durbin-Watson自相关性检测。这个算法的原理相对来说很简单，其实也就是找到数组中残差的自相关性，如式$5$：

$$d=\frac{\sum_{t=2}^T(e_t-e_{t-1})^2}{\sum_{t=1}^Te_t^2}\tag{5}$$

其中$e_t$指的就是第$t$时刻的数组元素。

用极端正负相关看看原理

我们举两个极端的例子，比如：

$$
\begin{matrix}
\mathbf{A}={\lbrace}&a_n&|&a_n=a+(n-1)\cdot d&|&d=1,n=1,2,…{\rbrace}\
\mathbf{B}={\lbrace}&b_n&|&b_n=a\cdot(-d)^{n-1}&|&d=1,n=1,2,…{\rbrace}\
\end{matrix}
\tag{6}
$$

也就是说：

$\mathbf{A}$是一个从$1$开始，依次递增$1$的等差数列，呈标准的正相关；

$\mathbf{B}$是一个从$1$开始，$1$和$-1$交替出现，呈标准的负相关。

P.S.：我特意要把公式写出来，是为了表明$\mathbf{B}$确实是负相关。

那么，对于$\mathbf{A}$，$e_t-e_{t-1}\equiv d=1$，于是，若取$T=100$，则有：

$$d_\mathbf{A}=
\frac{\sum_{t=2}^T(e_t-e_{t-1})^2}{\sum_{t=1}^Te_t^2}=
\frac{\sum_{t=2}^{100}1}{1^2+2^2+…+100^2}=
\frac{99}{\frac{100(100+1)(2\cdot100+1)}{6}}=
2.9\times10^{-4}
$$

同理，对于$\mathbf{B}$：

$$
\begin{matrix}
\exist t=2,4,6,…{\Rightarrow}e_t-e_{t-1}=-1-1=-2\
\exist t=3,5,7,…{\Rightarrow}e_t-e_{t-1}=1-(-1)=2
\end{matrix}
$$

因此，$(e_t-e_{t-1})^2\equiv4$，且$e_t^2\equiv1$。

于是，同样对于$T=100$，有：

$$
d_\mathbf{B}=
\frac{\sum_{t=2}^T(e_t-e_{t-1})^2}{\sum_{t=1}^Te_t^2}=
\frac{\sum_{t=2}^{100}4}{\sum_{t=1}^{100}1}=
\frac{4\times99}{100}=
3.96
$$

我们计算出了$d_\mathbf{A}$和$d_\mathbf{B}$。根据Durbin-Watson的规律，我们可以认定：

$d_\mathbf{A}<2$，则$\mathbf{A}$是正自相关；

$d_\mathbf{B}>2$，则$\mathbf{B}$是负自相关；

就是这么一回事。

回到主线任务

那么，对于我们的$f(x)=sin(x)$与$g(x)=cos(2x)+0.3$这两条曲线呢？

这个确实不太好计算。我们用程序来试试：

1
2
3
4
5
6
7
8
def calculate_dw_stats(samples):
    residuals = samples
    diffs = np.diff(residuals)
    return np.sum(diffs ** 2) / np.sum(residuals ** 2)
x = np.arange(0, 100, 1)
y = np.sin(x)
z = np.cos(2 * x) + 0.3
print(f"DW(y)={calculate_dw_stats(y)}, DW(z)={calculate_dw_stats(z)}")

输出的结果有些让人出乎意料：

1
DW(y)=0.909548742021243, DW(z)=2.3556147877841003

不过没事儿，会出现这样的结果其实也与采样是相关的。我们取得粒度有些大，就像这样：

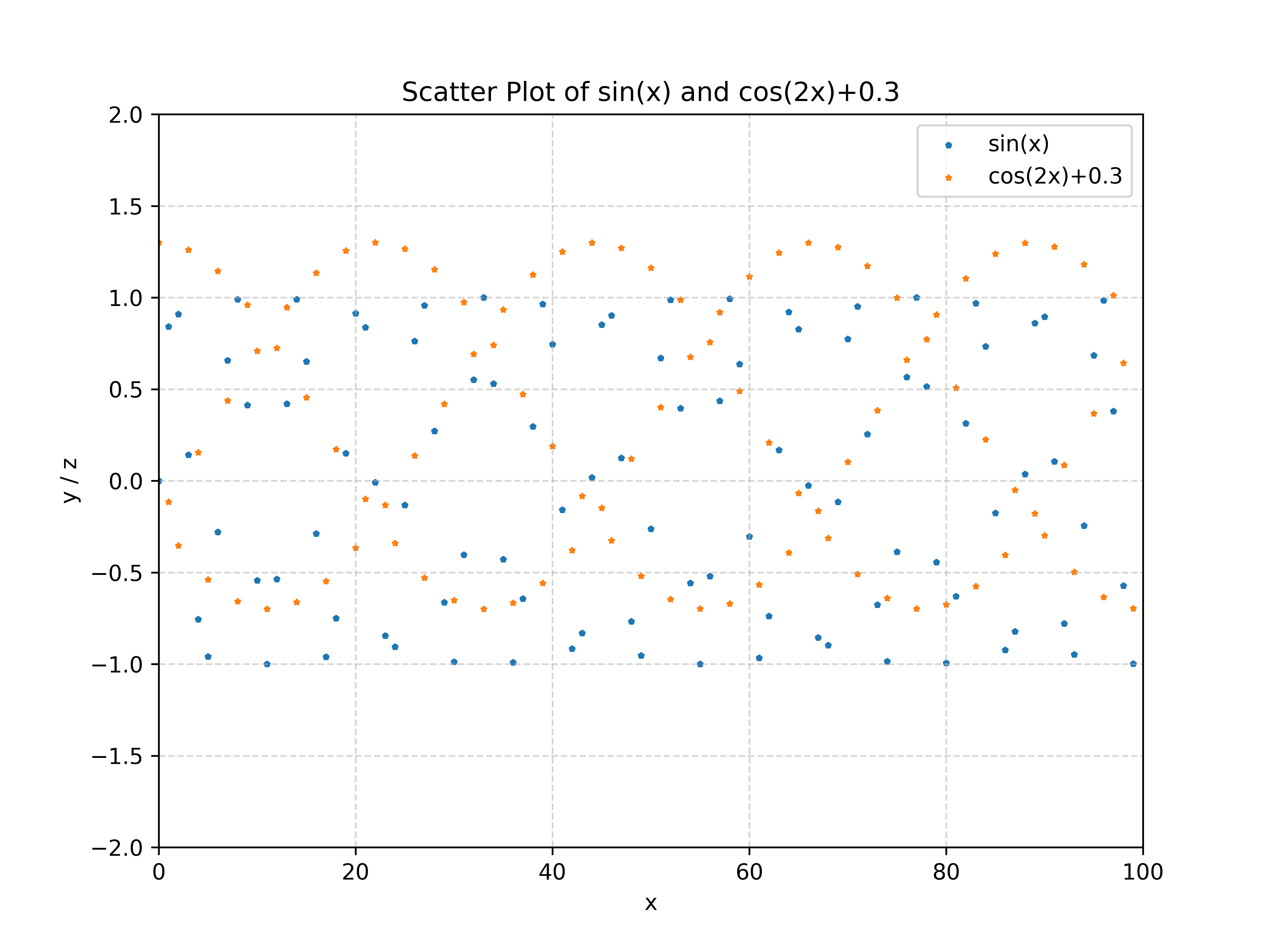
乱七八糟的散点

人眼其实勉强能够看出来一丁点规律，但是奈何计算出来的结果是一团乱麻。所以呢，我们就把粒度缩小一些，比如$0.1$，代码上就是这么改：

1
x = np.arange(0, 100, 0.1)

于是效果如下：

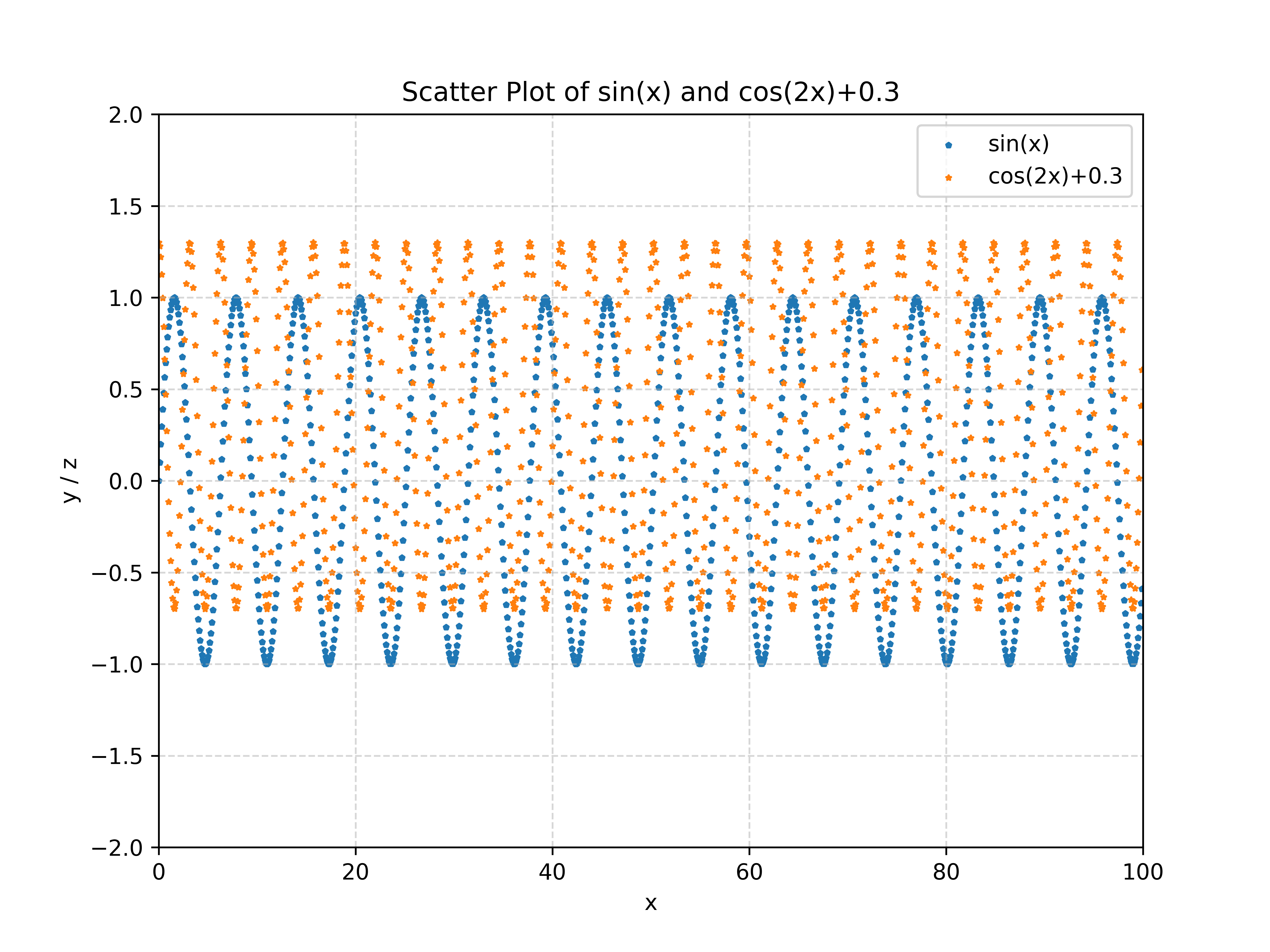
缩小粒度的散点

看起来好多了。

我们再算一次：

1
DW(y)=0.00989348517923295, DW(z)=0.033980931497872346

看着顺眼多了。大概不会再有偏差很大的值了，就相当于两个都有着很强的自相关性。

这也给我们带来了实践上的启发：粒度尽可能细、长度尽可能长，对于带有周期性质的数组，可以更好地捕捉到周期特征（也就是自相关性）。