合理看待矩阵运算与CUDA加速

发表于 更新于 分类于 阅读次数： 本文字数： 1.7k 阅读时长 ≈ 6 分钟

前言

首先声明，这是个整活。

想起来一个常见的题目：在一个数组中找到三个和为$x$的组合，并且去重。相信在座的各位大佬都已经不屑一顾了。最经典的三指针做法，核心就是先排序，然后暂时固定一个数字，剩下的两个数字用双指针从两边往中间缩，整体就是一个$O(n^2)$。

很多面试官当然也就摒弃那种暴力搜索方案，因为三个确实就是$O(n^3)$，时间消耗非常让人绝望。但是，暴力的代价真的很大嘛？

所谓力大砖飞，自然也就是矩阵运算了。

双指针

这里就不再介绍有的没的了，原理和代码已经遍地都是了。这里就单纯介绍结果。

我的硬件设备配置如下：

硬件 配置
CPU Intel Xeon E3-1245V3
GPU NVIDIA GeForce GTX 1660Ti（6G）
内存 ECC 16G DDR3-1600MHz

运行用例：从$-511$依次递增$1$，到$511$，共$1022$个数字，可能的组合包括$C^3_{1022}=177388540$种可能。

最终，耗时$60$毫秒。

$60$毫秒是什么概念呢？

我也尝试了最暴力的三层for循环，这个数量级和硬件条件下，使用的时间是$11.69$秒，双指针优化了大约$\frac{11.69-0.06}{0.06}=193.833$倍。

我们接下来看看矩阵的表现。

广播规则加速运算

在开始之前，矩阵运算为什么比我们想象中的快，这里面其实是有一些小技巧在的，也就是我们所说的numpy广播规则。

规则是什么就不再多说了，毕竟已经使用的很广泛了。

没有一点技巧，只有暴力

力大！砖飞！(๑•̀ㅂ•́)و✧

既然讲究纯粹的暴力，但是又想借用矩阵运算的高速并行，那么就可以这么想：

既然我有一个数组，要找三个数，那我们干脆把这个数组复制$2$份，一共$3$个一模一样的数组，组成一个三维空间，互相垂直相交，构成一个三维矩阵，矩阵中的每一个单元格里面保存的是三个数的和。

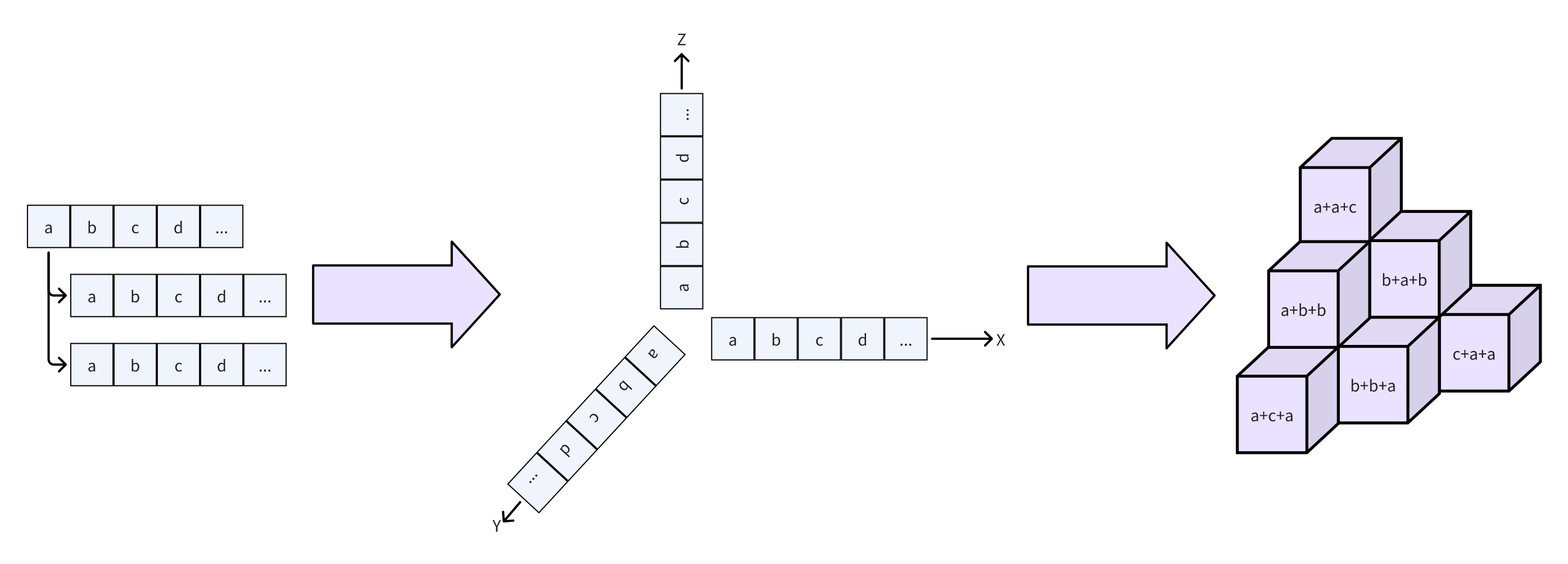
构建三维矩阵

确实可以说的上是极致的暴力了。

而这个过程实际上就是广播，将原本$n$个元素的数组拓展成$3$个，尺寸分别是$(n,1,1)$、$(1,n,1)$和$(1,1,n)$。这样也就让原本的数组可以拓展为三维矩阵。

然后，将这三个尺寸全部加起来，矩阵的每一个单元格就是数组对应位置的和了。

然后，找到三维矩阵中的数字是目标值的单元格索引，再回到原一维数组中查询原数字，即可找到组合。

那事不宜迟，开始写吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
from typing import List, Tuple
def find_triplets_cpu(
    arr: List[int], target: int
) -> List[Tuple[int, int, int]]:
    arr = np.array(arr)
    # 广播获得三元组
    sums = arr[:, None, None] + arr[None, :, None] + arr[None, None, :]
    # 找到和为target的索引
    idx = np.where(sums == target)
    # 过滤，并保证顺序
    triples = [(i, j, k) for i, j, k in idx if i < j < k]
    values = [(arr[i], arr[j], arr[k]) for i, j, k in triples]
    return values

似乎没问题。那么最终花了多少时间呢？

答案是绝望的$10.12$秒，比三重循环的暴力搜索也好不到哪里去。

力大……砖飞……o(╥﹏╥)o

从纸面数据上看，两者其实计算量都是$O(n^3)$。但从根本上来说，矩阵运算还是并没有那么快。

这个的话，其实主要问题处在内存访问上。

如果说，一个数据从内存里面摘出来，然后立即丢弃，这个响应速度其实是相当快的。

但，不幸的是，这个三维数组的大小，在这台机器上，占据了惊人的$4123.8\text{MB}$。

还记得上面的硬件配置吗？现在用的是DDR3-1600MHz的内存，搬运数据的速度大约是$12.8\text{GB/s}$。我们计算一下，如果是这么大的数据，需要

$$\frac{4123.8\text{MB}}{12.8\times1024\text{MB/s}}=0.31462097168\text{s}=314.62097168\text{ms}\tag{1}$$

光读取就去掉$300$毫秒。

所以，力大，有可能房子都塌了，砖飞不飞也无所谓了。

没办法了？

就到此为止了？$12.8\text{GB/s}$是内存的极限罢了。

难道说，还有高手？

当然，该显卡出手了。

显卡是$388\text{GB/s}$，比CPU可优秀多了。那，就用上PyTorch的张量计算吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
def find_triples_gpu(
    arr: List[int], target: int
) -> List[Tuple[int, int, int]]:
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    x = torch.tensor(arr, device=device)
    n = x.size[0]
    sums = x.view(n, 1, 1) + x.view(1, n, 1) + x.view(1, 1, n)
    idx = (sums == target).nonzero(as_tuple=False)
    keep = (idx[:, 0] < idx[:, 1]) & (idx[:, 1] < idx[:, 2])
    idx = idx[keep]
    tuples = [tuple(t.tolist()) for t in idx.cpu()]
    values = [tuple(arr[i] for i in t) for t in tuples]
    return values

其实方式大差不差，只是单纯的将运算放在了显卡里面。

这个时间是多少呢？

答案是恐怖的$790$毫秒。相对于CPU算法而言，这种方法提升了$11.924$倍。

还是相当可观的。

但是相比双指针，这种方法还是差了$10$倍不止。别的不说，人家双指针的计算量还是要少一个量级的。

没办法了……

其实到这里确实是三维矩阵的极限了。

计算量下不去的话，时间是无论如何也下不去的。能继续缩减的无非就是二维矩阵了。

当然，二维矩阵加上Python的for循环，反复将数据在C语言与Python解释器中来回提交，也不是个办法。更不用说PyTorch还得将数据移交显卡，CPU与GPU的切换只会更绝望。

所以，能用上二维矩阵的也就只有CPU了。

于是，参考双指针的思想，先确定其中一个，剩下的用二维矩阵找出所有匹配的内容，然后用掩码寻找索引。就像这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from typing import List, Tuple
def find_triplets_cpu(
    arr: List[int], target: int
) -> List[Tuple[int, int, int]]:
    arr = np.asarray(arr)
    n   = len(arr)
    triples = []
    for i in range(n - 2):
        rest = arr[i + 1:]
        need = target - arr[i]
        sums = rest[:, None] + rest[None, :]
        mask = np.triu(sums == need, 1)
        js, ks = np.nonzero(mask)
        triples.extend([
            (i, i + 1 + j, i + 1 + k) for j, k in zip(js, ks)
        ])
    return triples

测试运行时间：$0.59$秒，甚至比显卡的极限还要极限。

到这里，也就确实是极限了……

……吗？

当然，再优化就又回到动态规划了，到头来还是双指针。

所以，到这里也没活整了。

到这里再回看标题：合理看待矩阵运算与CUDA加速。到头来，如果计算量级没办法降，用再多的矩阵运算还是无法突破极限。