面试记录：怎么理解多头注意力机制

发表于 2025-08-26 更新于 2025-09-01 分类于 interview 阅读次数：本文字数： 1.4k 阅读时长 ≈ 5 分钟

简介

当然，大模型有很多注意力，毕竟Attention is All You Need。但是呢，自注意力，多头注意力，这些又是什么？怎么串在一起的？

自注意力

在无线网络质量分析的过程中，我们往往会注意到无线网络的RSRP数值随着时间变化的过程。而如果我们需要利用这个分析去预测下一个时间片的RSRP数值时，我们就一定会使用若干之前时间片的RSRP数值作为参考，向后预测。

这种数据，我们就称其为自相关的数据。因为，RSRP除了和时间有关系之外，还和之前的自己有关系。

自注意力的本质就是如此。

传统过程

为了实现自注意力，比较直观的方法其实是RNN、LSTM这些。参考这篇文章的说明，其实也就是将下一个数据的预测过程表达为$\mathbf{C}t $与$ \mathbf{C}{t-1}$之间的线性关系。

但是很明显，时刻的数值必须等待时刻的数值计算完毕，并行效果一般。

新方法

为了弥补传统过程中计算慢的问题，有人提出了一个新的算法，就是平常使用最多的：Scaled Dot-Product Attention。

他的流程如下：

graph LR
  A[MatMul]
  B[MatMul]
  Q-->A
  K-->A-->C[Scale]-->D[mask: Optional]-->B
  V----->B-->E[Output]

这个公式也是相当出名了：

其中，Q、K、V分别表示查询、键、值。d_k表示键的维度。Scale表示将除以。mask表示是否进行遮罩。Output表示输出。

在这里，Q可以理解为我现在需要问的问题；K可以理解为现在知识库里面所有知识的标签。V可以理解为知识库里面标签对应的所有知识的内容。

我们通过三个可以学习的参数，记为、、，、、的由来其实就是输入问题与参数的线性变换：

于是，注意力就可以表示为：

最终的输出经过softmax修整后，也就成为了概率。

这个概率最终对应到的物理意义，本质上就是和之间的相似度，也就是下一个token取的概率。这个概率可以表示为：

不难看出，概率本质上也是句子中第个位置和第个位置的相似度，因此用二维表表征相关性矩阵。

多头注意力

上面的自注意力讲述了单头注意力如何表现，多头注意力也就是实现了多个单头注意力，然后进行拼接。

多头注意力的流程如下：

graph LR
  A[MatMul]
  B[MatMul]
  F[MatMul]
  G[MatMul]
  Q-->A
  K-->A-->C[Scale]-->D[mask: Optional]-->B
  V----->B
  K-->F
  Q-->F
  F-->H[Scale]-->I[mask: Optional]-->G
  V----->G
  B-->L[Concat]
  G-->L
  L-->M[Linear]

当然，mermaid画出来可能不太直观。我们换一张图：

MHA

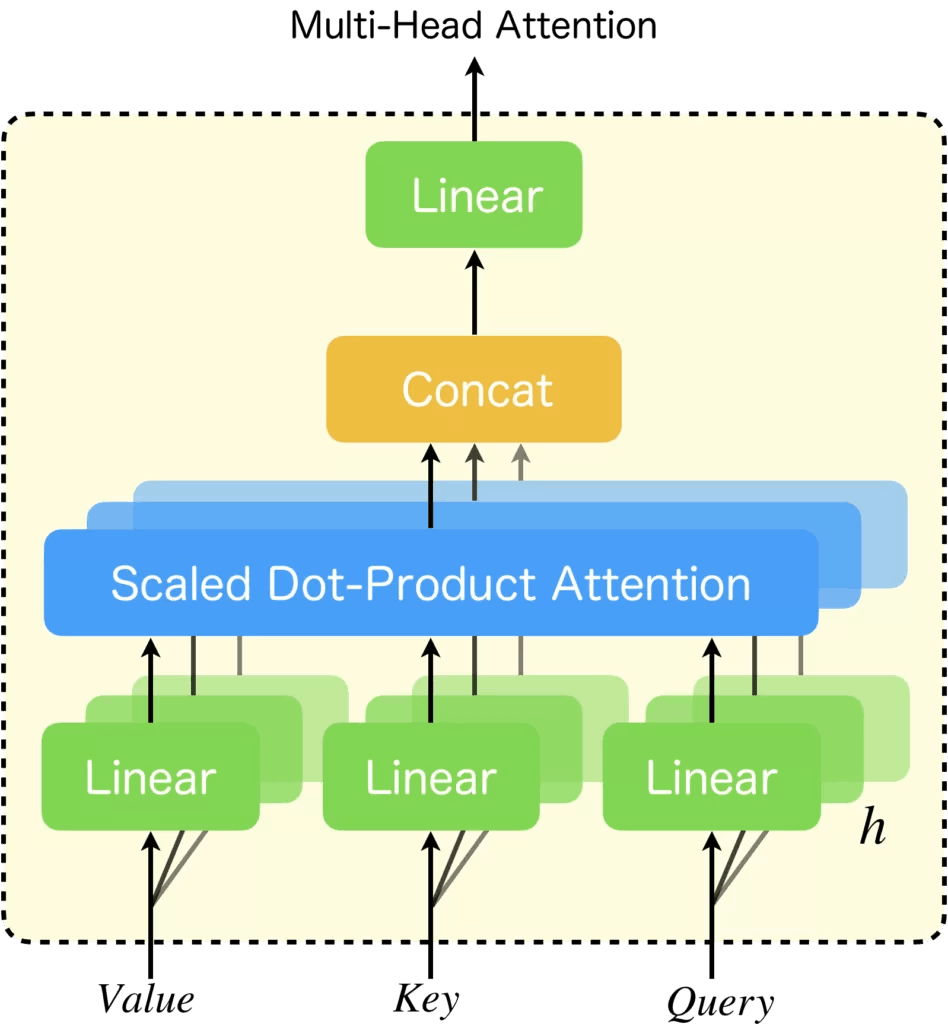
摘自文章：https://zenn.dev/yuto_mo/articles/72c07b702c50df

作者：@yuto

可以看到，多头注意力在本质上，其实就是采用了多个Scale Dot-Product Attention，并将结果拼在一起作为输出。

也就是说，有式：

（将多头注意力记为MHA，单头注意力记为A）

每一个单头注意力都可以注意到句子中的一部分语义，因此多头注意力也可以识别到更多的信息。

因果mask

在很多博客中，都会提到这个词。这个词在GPT任务中，将限制模型查看上下文信息，从而保证生成内容的方向是始终一致的，也就是逐字追加。

上面的流程图中，mask标记的是Optional，其实也并不是说可以省略，只是单纯的因为，机器翻译是不需要这个mask的。

对于GPT，mask的实现本质上也就是限制遍历对象：

其中，mask就是其中的M_{ij}，表示为：

其中，取时，表示因果遮罩要求模型只能够关注到自己和左侧的元素，而取时，返回值是，代入式，显然，所以对模型来说，就是将的元素置零，从而屏蔽当前位置右侧的所有元素。

于是，这个句子就很自然而然地构成了下三角矩阵。

比如，当前输入的内容是：你是一只猫娘。

那么矩阵就会变成：

	你	是	一	只	猫	娘
你	1	0	0	0	0	0
是	1	1	0	0	0	0
一	1	1	1	0	0	0
只	1	1	1	1	0	0
猫	1	1	1	1	1	0
娘	1	1	1	1	1	1

当然，这里不会真的都是，我写只是为了占个位置而已，实际上这里的都应该是之间的一个数，而的位置就是。